昨天看到一条推文，内容如下：

2019年5月23日になりました。

20190523→素数
0190523→素数
190523→素数
90523→素数
0523→素数
523→素数
23→素数
3→素数

どこから左を切っても素数となる珍しい日です！

说的是 2019 年 5 月 23 日是一个不同寻常的日子，因为日期对应的数字 20190523 是一个素数（质数），同时这个数字去掉左边任意位数字后，剩下的部分都仍然是素数。因此，这一天可以被称为“素数日”。

看到这个推文，我有点好奇，像 20190523 这样的素数日究竟有多罕见呢？于是便写了一段程序穷举了一下，将 2000 年 1 月 1 日开始的 1000 年的日期都校验了一遍，发现在这长达 365243 天的一千年里，一共只有 53 个素数日，比例差不多是万分之 1.5。这 53 个日期如下：

20000107  2000年01月07日
20000503  2000年05月03日
20010223  2001年02月23日
20010313  2001年03月13日
20031223  2003年12月23日
20060107  2006年01月07日
20070823  2007年08月23日
20100907  2010年09月07日
20130223  2013年02月23日
20190523  2019年05月23日
20190823  2019年08月23日
20300317  2030年03月17日
20360317  2036年03月17日
20400307  2040年03月07日
20400823  2040年08月23日
20480107  2048年01月07日
20600317  2060年03月17日
20660617  2066年06月17日
20700103  2070年01月03日
20700223  2070年02月23日
20700307  2070年03月07日
20700523  2070年05月23日
20721013  2072年10月13日
20910103  2091年01月03日
20930113  2093年01月13日
21000313  2100年03月13日
21000907  2100年09月07日
21050503  2105年05月03日
21320107  2132年01月07日
21330313  2133年03月13日
21360223  2136年02月23日
21870223  2187年02月23日
21890107  2189年01月07日
21990523  2199年05月23日
23000617  2300年06月17日
23010313  2301年03月13日
23100313  2310年03月13日
23970313  2397年03月13日
24021013  2402年10月13日
24050503  2405年05月03日
24090907  2409年09月07日
24270223  2427年02月23日
24350503  2435年05月03日
24501223  2450年12月23日
24900307  2490年03月07日
26001013  2600年10月13日
26070313  2607年03月13日
26150503  2615年05月03日
26190313  2619年03月13日
26931013  2693年10月13日
27020113  2702年01月13日
27080107  2708年01月07日
29331013  2933年10月13日

万分之 1.5 的比例的确是很稀少的，因此素数日是一个少见的特殊日子。幸运的是，今年有两个素数日，除了刚刚过去的 2019 年 5 月 23 日之外，再过三个月的 2019 年 8 月 23 日（20190823）也是一个素数日，而再下一个素数日则要等到 11 年之后的 2030 年 3 月 17 日了。

既然已经写出了代码，当然不妨把穷举的日期范围再扩大一点。于是，我验证了从公元 1 年 1 月 1 日开始到公元 9999 年 12 月 31 日这一万年内的所有日期，发现素数日共有 815 个，占比大约为 0.02%，或者说万分之二。

这 815 个素数日的分布并不均匀，如果以世纪为单位，可以得到下面的图：

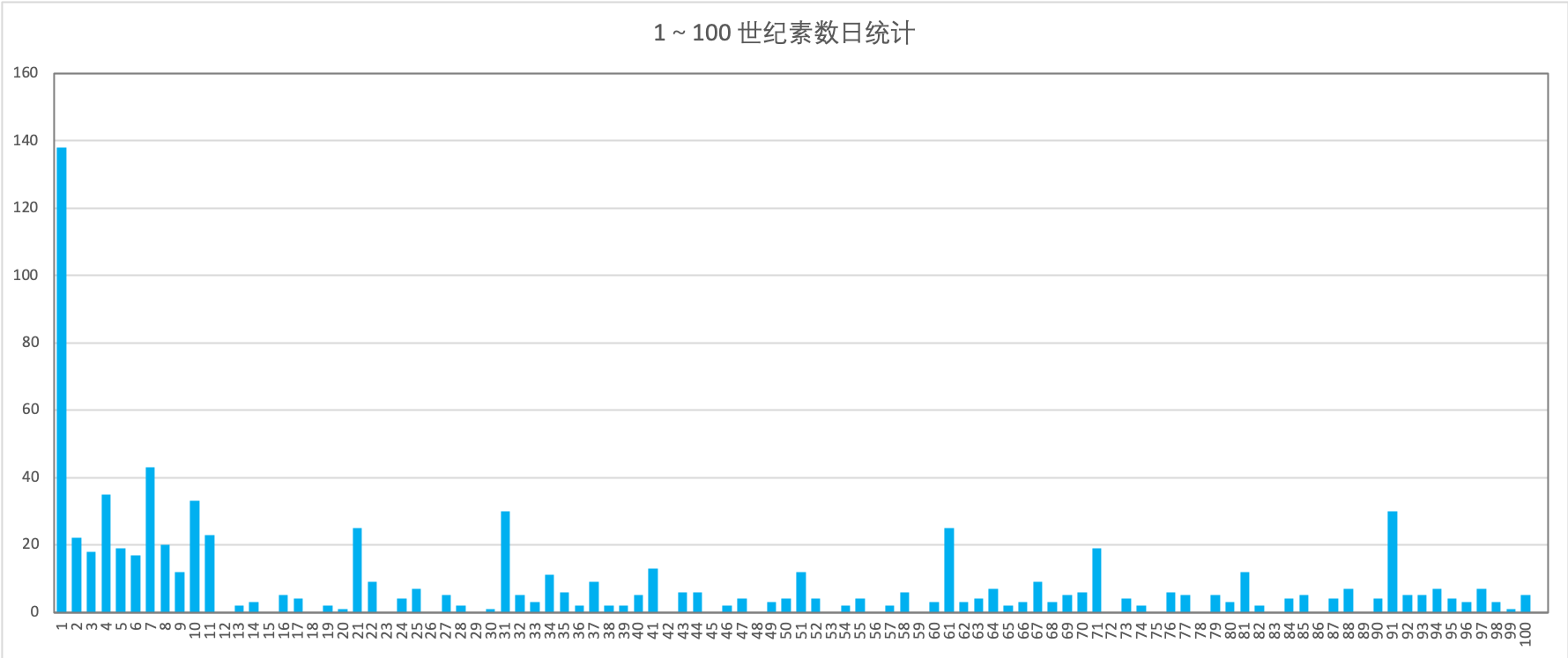
可以看到，公元 1 世纪 ～ 10 世纪素数日都挺多，之后则是每个 X1 世纪（比如 21 世纪、31 世纪）素数日比较多，有一些世纪则整整 100 年都没有一个素数日，比如 23 世纪、26 世纪都没有素数日。

这么看来，我们生活在 21 世纪还算是比较幸运的，因为这是一个 X1 世纪，这 100 年里的素数日有 25 个之多，基本上占了所有 2XXX 年里素数日数量的一半。

2021-01-14 补充： 原来这种可以从一边去掉任意连续数字后仍然是质数的质数，叫可截短质数，分为可左截短质数和可右截短质数。令人惊讶的是，这种数字是有限的，其中十进制的可左截短质数共有 4260 个。