读《魔鬼数学》

《魔鬼数学》是一本关于如何使用数学思维来分析生活中一些常见问题的书,英文原名为《How Not to Be Wrong》,即本书中包含的数学思维可帮助读者避免一些错误。
下面是一些我读过之后的一些笔记以及感想。
日常练习的意义
这本书的引言部分提了一个问题,即日常做各类数学题有什么意义?
相信大多数人当初在学校时都思考过这个问题,每天做不完的题,除了把人训练成解题机器之外,真的有意义吗?
作者使用了体育训练的例子来回答这个问题,比如想踢好足球,达到职业水准,就必须接受大量枯燥、重复、看似无意义的训练,比如举杠铃、在交通锥之间穿梭前进。职业运动员在比赛中不会用到这些训练内容,但是他们所表现出来的高超的力量、速度、观察力、柔韧性等能力,则是这些枯燥乏味的训练的结果。
学数学以及其他任何一门学科也是类似,每日刷题等练习看似枯燥且无用,但这和职业运动员每日做基础的体能、反应训练的逻辑是一样的,如果你真的想在这个领域成为专家,这样的训练必不可少。
非线性
A 国在讨论是否要提高福利,有人反对,理由是以高福利著称的 B 国最近正在削减福利,如果提高福利是好事,那 B 国为什么要削减福利呢?
这个反对意见的问题在于,提出者认为福利与国家的繁荣程度是线性关系,如下图:
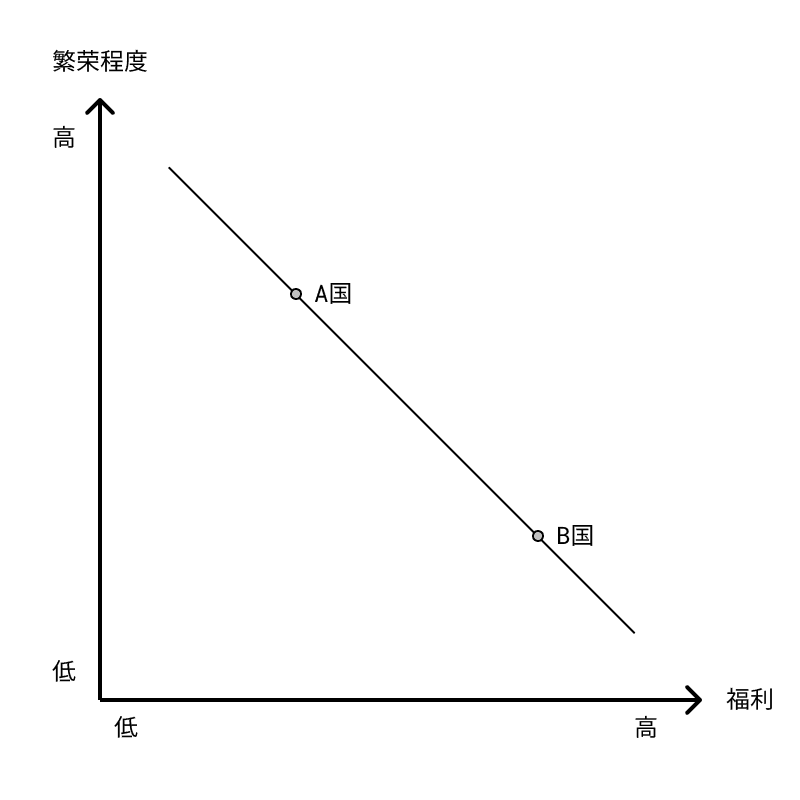
如果现实真的是这样,那么的确如反对意见所说,越是降低福利,国家的繁荣程度就会越高。然而现实世界中大多数事物之间并不是线性关系,繁荣程度与福利水平的真实关系更可能类似下图这样:
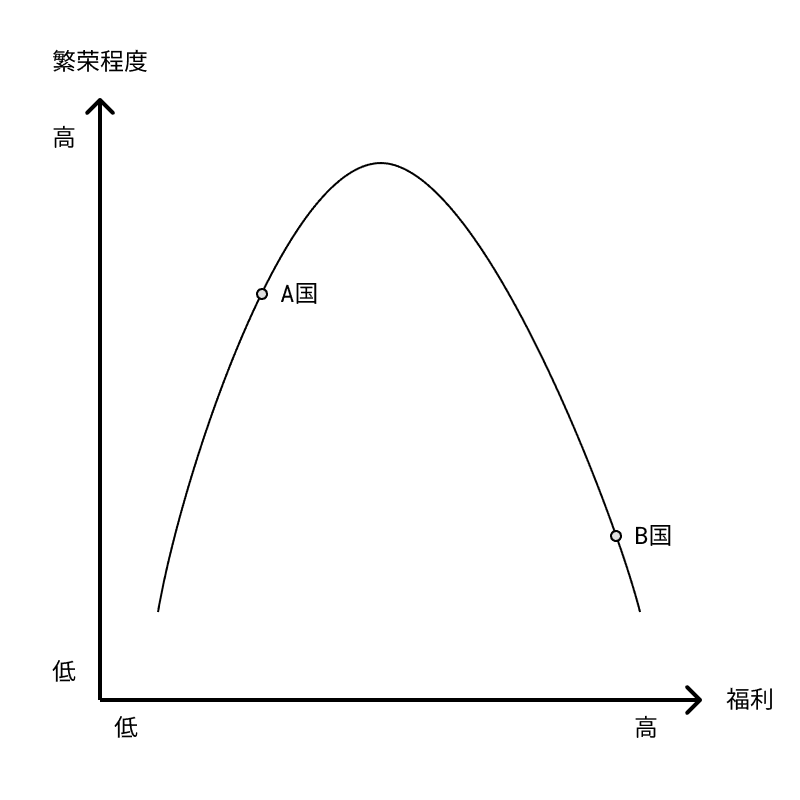
可以看到,繁荣程度-福利水平关系是一条上凸的曲线,A、B 两国分别位于峰值的两边,此时对 B 国来说削减福利能提升繁荣程度,但对 A 国来说却相反,增加福利才是最佳选择。
因此,在一个非线性的世界,我们不能不加思考地照搬人家的经验,不能因为其他人做了某个选择取得了成功,就认为我们照着做也能成功,因为世界不是线性的,我们所处的位置不一样,努力的方向就可能也不一样。
小概率事件
有一个著名的小故事,讲的是一位股票经纪人每周给一批人发送行业资讯,一半的人收到的消息是某只股票将会涨,另一半人收到的则是那只股票会跌,下一周则不再理会收到错误预测的那一半人,继续给另一半人发新的预测资讯。这样几次之后,总有一小部分人惊讶地发现这位经纪人每次都能说对,于是对他言听计从,此时,股票经纪人就会开始收网,劝说这些人买入他指定的股票,从而大赚一笔,当然,最终赚钱的永远是股票经纪人自己。
只要这位股票经纪人一开始联系的人足够多,总有一部分“幸运儿”会发现自己遇到了一位神奇的预测大师,但站在股票经纪人的角度来看,这一切其实一点也不稀奇。
我们生活中可能会遇到很多类似的事,只是有一些做了若干包装或者改进,让人不那么容易看出真相。比如基金公司可能会同时孵化多支基金,尝试无数种投资策略,只要孵化的数量足够多,这些基金中必然会有一些能在过去一段时间的市场中表现良好,然后基金公司就将其推出,向公众兜售。作为投资者,你看到某个基金过往的业绩如此耀眼,你是否会心动呢?
不排除有一些投资策略的确比另一些更有可能赚钱,但孵化大量基金并推出其中表现良好那些的做法,本质上与上面股票经纪人的做法是一样的。这些最终胜出的基金,有可能只是运气好,没有人能保证它们在今后的市场中还能有这样的好运气。
有一些研究者曾声称在圣经等典籍中发现了隐藏的密码,比如只要每隔多少个字符取一个字母,就能拼出后世某位名人的名字以及他的生卒年月等信息,这也是一种类似的把戏。从长篇巨著中寻找字母有无数有找法,只要你尝试得足够多,你总能从中找到一些看起来有意义的组合,而另外无数种无意义或错误的组合自然而然地被你忽略了。
甚至,一些看似经过严格科学分析的结论也有可能受到随机性的影响,比如下面这幅漫画所描写的。

假设豆胶糖与痤疮没有关系,但只要科学家们做的试验次数足够多,总会遇到某些随机因素使实验者得到二者有关的结论,甚至可能还会具体到认为豆胶糖的颜色是主要原因,比如“吃绿色的豆胶糖与得痤疮之间有关系”。即使试验次数很少,比如只做了一次试验,也有可能因为随机性刚好得到两者相关的结论。
回归
很多事物都有回归均值的倾向,比如整体来看,子女成年后的身高与他们的父母相比更加趋于平均水平。
这样的例子还有很多,比如父母都很高,生的孩子并不是必然也高,有可能比父母矮一些,智力水平也一样,一对名校夫妇的子女可能无法像父母一样杰出。
又比如一个公司曾经非常赚钱,但后来却慢慢平庸,一位作家写出了惊艳的作品,下一部作品却反响平平,一个球队上一个赛季表现优异,下一个赛季却辉煌不再。
这些情况,也许并不是当事人取得一次成功之后就不再努力了,而是因为之前的优异表现是随机产生的,现在相关的指标只是回归到了均值水平而已。
相关性
如果 A 与 B 相关,B 与 C 相关,那么 A 与 C 相关吗?
这个问题即问相关性有没有传递性,按多数人的直觉,答案大概是肯定的,既然 A 与 B 相关,B 与 C 相关,那似乎很自然地 A 与 C 也是相关的。
这儿我们不深究“相关”一词的定义,只需大致知道这是一个统计学上的概念,默认是指正相关,即如果说 A 与 B 相关,则表示当观察到事件 A 发生时,我们相信事件 B 会有更大的概率发生,同时需要注意,相关关系并不是因果关系。
书中指出,如果我们把某个事件的相关数字看作坐标,则一个事件可以看成为某个高维空间中的点,从原点出发画一个箭头指向这个点,这个箭头被称为“向量”。
这样一来,我们就把事件转为了高维空间的向量,并且可以很快得出一些关于相关性的几何意义的结论。从几何上来说,相关性就是两个向量夹角的余弦。两个向量间的夹角越小,说明它们的相关性越大,夹角越接近 90 度,则表示两个事件越不相关,夹角刚好为 90 度时我们认为这两个事件是独立事件,夹角大于 90 度时则认为这两个事件是负相关,即两个事件不太可能同时发生。
这是一个理解相关性的极佳的视角。
此时,我们再来看一下最初的问题,如果 A、B、C 三个事件的关系如下图所示:

为简便起见,我们假设三个向量是在同一个平面中。可以看到,事件 A 与 B 之间的夹角小于 90 度,说明它们是相关的,事件 B 与 C 之间的夹角也小于 90 度,说明它们也是相关的,但是事件 A 与 C 的夹角却大于 90 度,说明它们是负相关的。也就是说,相关性并不能简单地传递,如果我们只知道 A、B 相关且 B、C 相关,对 A、C 之间的相关性我们并不能下结论。
举一个例子,比如甲持有 S1、S2 两支股票,乙持有 S2、S3 两支股票,丙持有 S3、S4 两支股票。
显然,甲乙的收益情况有一定相关性,比如 S2 股票大涨两人都会赚钱,乙丙的收益情况也有一定相关性,比如 S3 股票大跌两人都会赔钱,但甲丙两人的收益则可以认为完全无关,因为两人所持的股票组合完全不重叠。
最后,关于相关性,作者态度非常谨慎。他指出,如果我们发现自然界或社会中两个事件之间不存在相关性,这并不表示两个事件之间毫无关系,可能只是我们现在的研究方法尚不能揭示出它们之间的关系。
投票
一个群体经常需要对某些选择进行表决,一个朴素且大部分人都认同的原则是“少数服从多数”,即对备选项进行投票,得票多的方案胜出。
但是,“少数服从多数”的原则虽然看起来很简单,却也只在选项只有两项时才能取得最佳效果,只要选项多于两项,大多数人的喜好就可能自相矛盾。
比如有 A、B、C 三个选项,大家对这三个选项的态度是这样的:
| 人数占比 | 偏好排名 |
|---|---|
| 34% | A > B > C |
| 33% | B > C > A |
| 33% | C > B > A |
如果让大家进行投票,只能选一个选项,那么根据上表,会有 34% 的人选 A,33% 的人选 B,33% 的人选 C。选项 A 得到的支持最多,胜出。
但是仔细观察上表,我们可以看到除了第一行的 34% 的人,在另外 66% 的人心中 A 都是最差的选项,也就是说我们通过“少数服从多数”的原则,选出了对绝大多数人而言最差的那一项!
再看上面的表格,假如选项 C 不存在:
| 人数占比 | 偏好排名 |
|---|---|
| 34% | A > B |
| 33% | B > A |
| 33% | B > A |
显然,选项 B 将以绝对优势获胜。这时再将 C 加进去:
| 人数占比 | 偏好排名 |
|---|---|
| 34% | A > B > C |
| 33% | B > C > A |
| 33% | C > B > A |
结果按“少数服从多数”的原则,虽然 C 没有胜出,但原来的获胜者 B 也被淘汰了,胜利的桂冠落在了 A 的头上。也就是说,有些时候,加入一个精心设计的新选项,竟然会让原本有着绝对优势的方案落选。
为了解决这些的问题,先贤们设计了无数种更为精巧、复杂的投票方式,但遗憾的是每一种都有其不足,都会在某些情况下得到糟糕的结果。
究其原因,书中提到:
民意是根本不存在的东西,更准确地讲,只有在大多数人意见一致时民意才会存在。
个人的理解,如果用某种方法将群体的偏好映射成高维空间中的几何图形,那么大多数情况下这个图形应该是极为复杂的,而投票就是一种将这个图形“降维”投影到低维的方法。除非原始的高维图形本来就足够简单,否则只要投影的角度有所不同,得到的图形必然会大相径庭。
那么,是否存在完美的投票方案呢?是存在但还未被发现,还是从理论上就不存在?
作者进行了很长篇幅的探讨,从欧几里得的第五公设,聊到罗素的集合论悖论,再聊到哥德尔的不完备定理,最后给出了他的结论:
只要选举制度遵循……那个表面看似不容置疑的公理(如果多数人对 A 的支持度超过对 B 的支持度,那么 B 就不可能成为赢家),就有可能掉进自我矛盾的陷阱。
也就是说,完美的投票方案也许从理论上就不存在。
小结
除了确定性,数学也是人们用于思考不确定性的手段。借助数学知识,我们即使无法完全驯化不确定性,至少可以使它变得易于驾驭。
在白天时,尽可以相信自己的理念是正确的,但是到了晚上,则请认真思考自己的理念是不是错误的。
数学告诉我们:世界是有结构的;我们可以期待去了解它的部分结构,但不可能像我们想象的那样一蹴而就;在披上形式主义的外衣之后,我们的直觉将会变得更加强大。
数学是常识的衍生物,有的活动虽然没有被表示成一个方程式,或者被画成一幅图,却同样属于数学活动。
评论:
你好,请问我可以将这篇文章转载到我的qq空间日志里吗?
可以啊。
B和C选项是67%的人心中最差的。所以并不是选出了绝大多数人而言最差的那一项吧。所以可能举例是不那么恰当吗?
你说的是这个表吗?哪里看出“ B 和 C 选项是 67% 的人心中最差的”呢?
第一行表示有 34% 的人认为 A 好于 B 好于 C,第二行表示有 33% 的人认为 B 好于 C 好于 A,第三行表示剩下 33% 的人认为 C 好于 B 好于 A。除了第一行 34% 的人认为 C 是最差的,其他人那里 B 都不是最差的,应该不会有“ B 和 C 选项是 67% 的人心中最差的”结果?