作为一名半路出家的程序员，我一直没有弄明白计算机是怎么实现加法操作的，直到最近读了《编码》这本书。

下面，是我对加法器原理学习的小结。

1、继电器

做加法器首先需要需要各种逻辑门，而实现逻辑门的一个关键部件是继电器。虽然现代计算机已经使用效率更高的半导体代替古老的继电器，但基本原理并没有变化，追本溯源，我们的加法器仍然从最基础的继电器开始。

下面是一个电磁铁。如果闭合开关，右边那个线圈缠绕的铁柱会产生磁场。

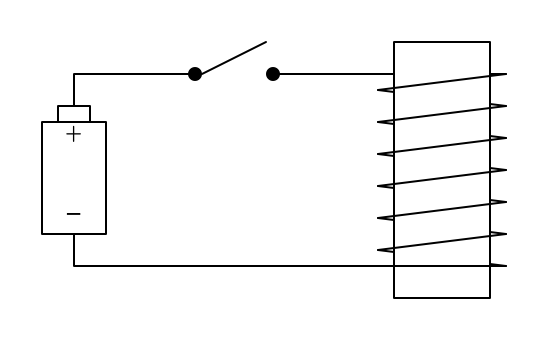
有了电磁铁，我们就可以制造出如下的装置：

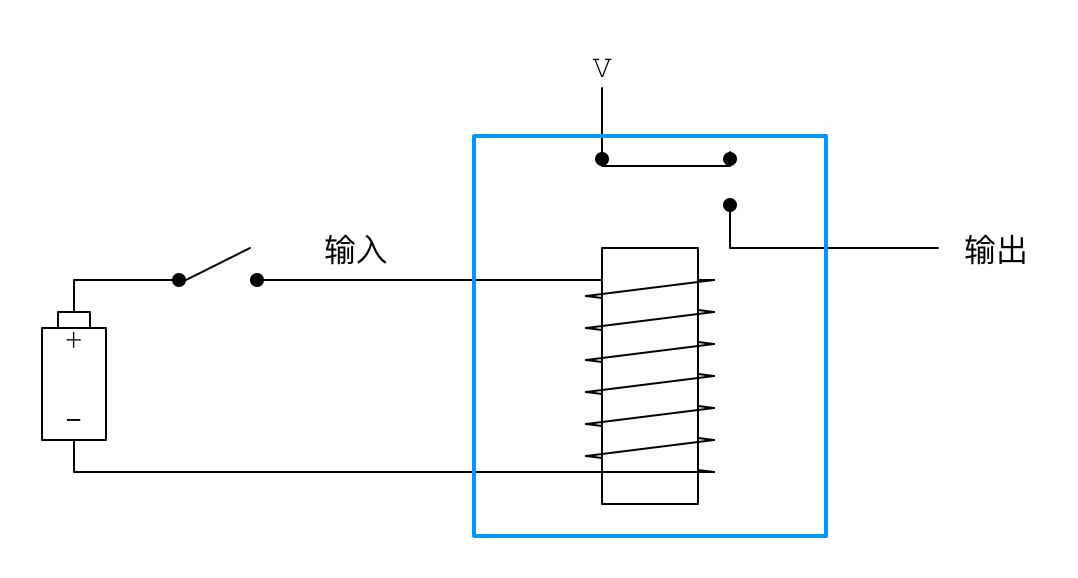
这个装置的特别之处在于，通过对电磁铁线路开关的打开和闭合，我们可以控制另一个线路的开关。比如，当闭合电磁铁的开关时，电磁铁会将右边的开关吸下来，接通右边的线路，如下图所示：

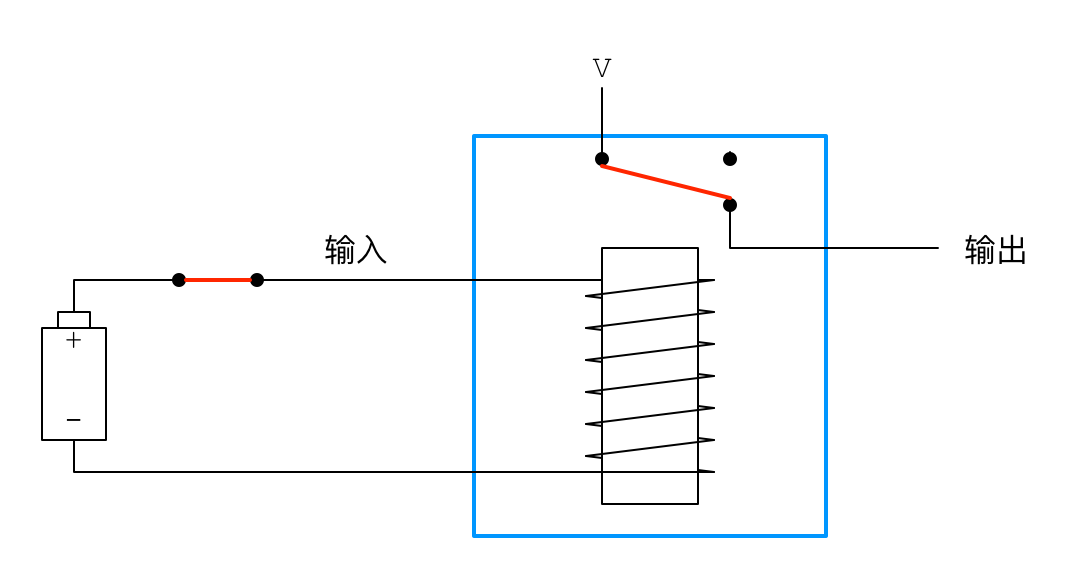
这个装置蓝色线框中的部分，就被称为继电器。

2、逻辑电路

电路有两种基本连接方式：串联和并联。

下图中的两个开关是串联：

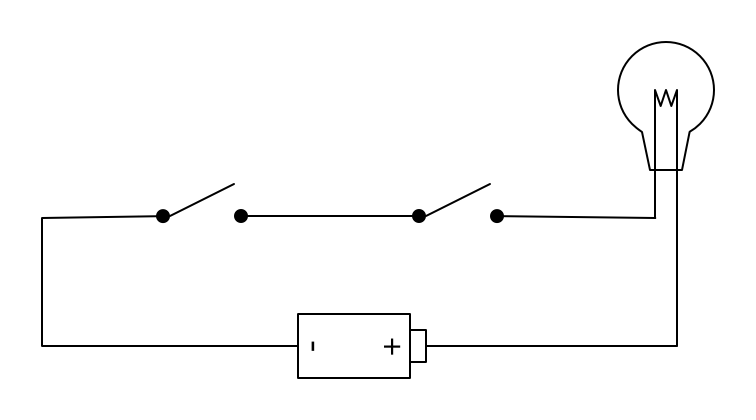
在串联的电路中，两个开关必须全部闭合，整个电路才能接通：

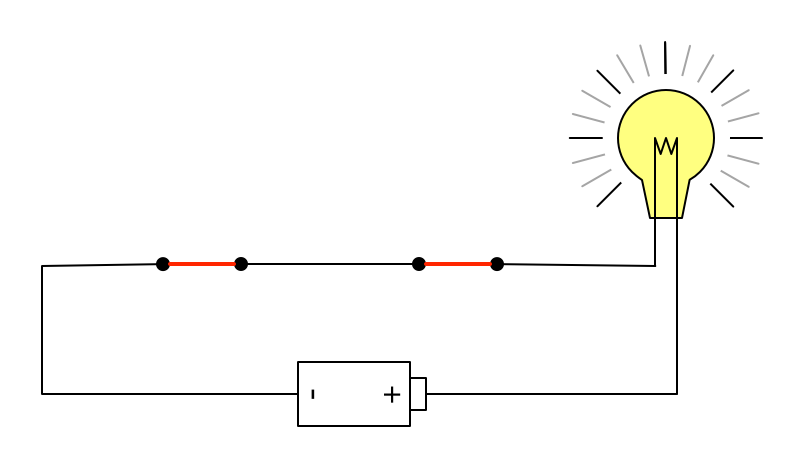
简单来说，串联对应着逻辑与（AND）操作。

对应的，下图中的两个开关是并联：

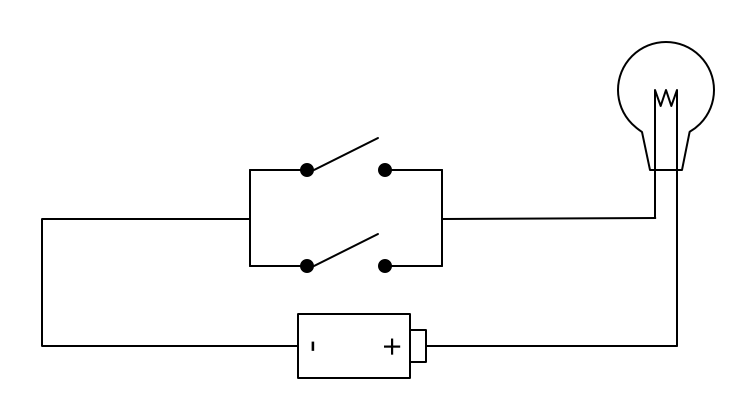
在并联的电路中，只要有任意一个开关闭合，整个电路就能接通：

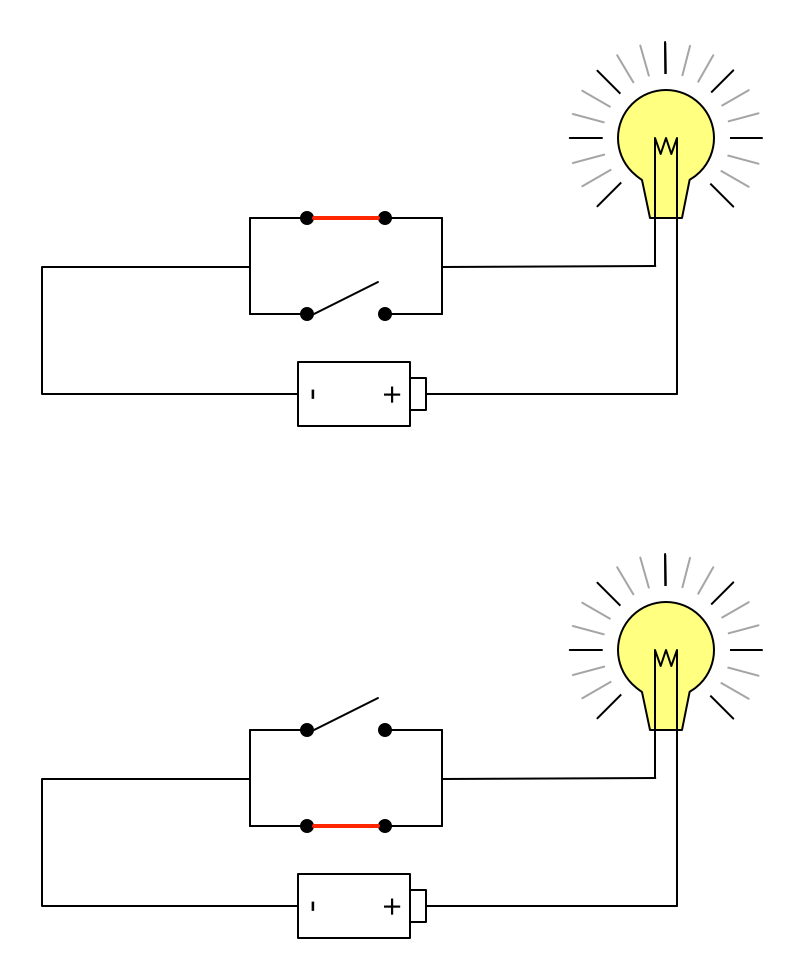
并联电路对应着逻辑或（OR）操作。

3、门

与门

如果我们将两个继电器串联起来，就能得到一个与门：

<img" src="/uploads/2017/04/e4b88ee997a81.png?w=1534" alt="与门1" width="767" />

只有左边两个开关同时闭合时，右边的灯泡才会被点亮。

与门可以简记为下面的符号：

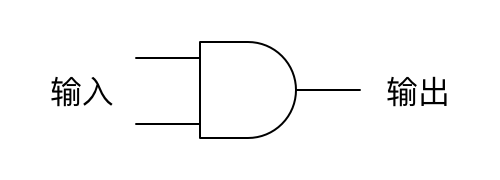
使用这个符号，可以将上面的电路图简化为这样：

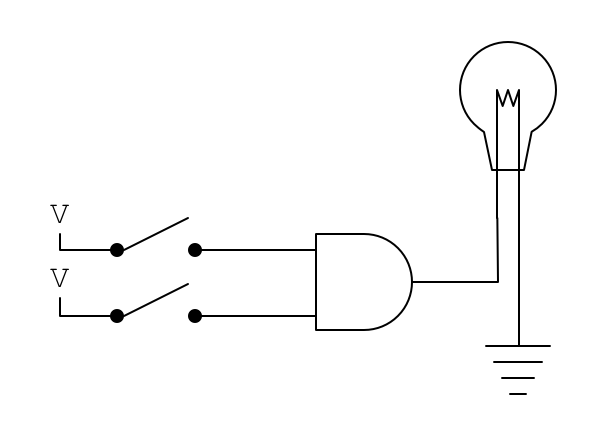
如果用 0 表示线路断开，1 表示线路连接，那么与门的输入与输出共有以下 4 种情况：

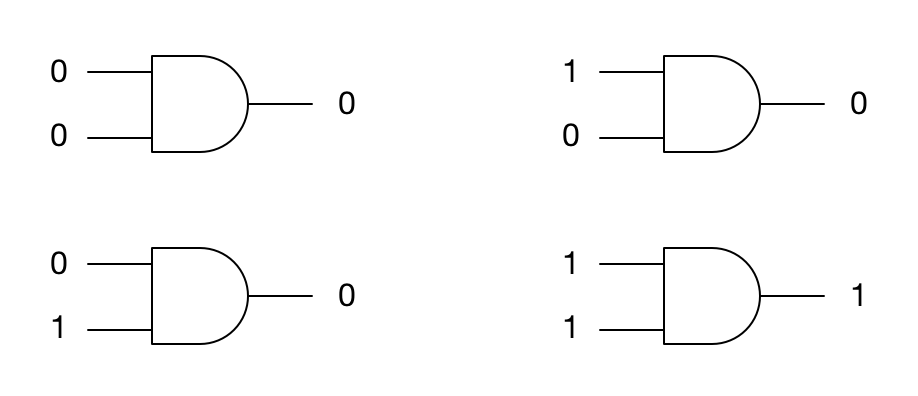
这些关系可以用下表来描述：

AND	0	1
0	0	0
1	0	1

或门

将两个继电器并联，可以得到一个或门：

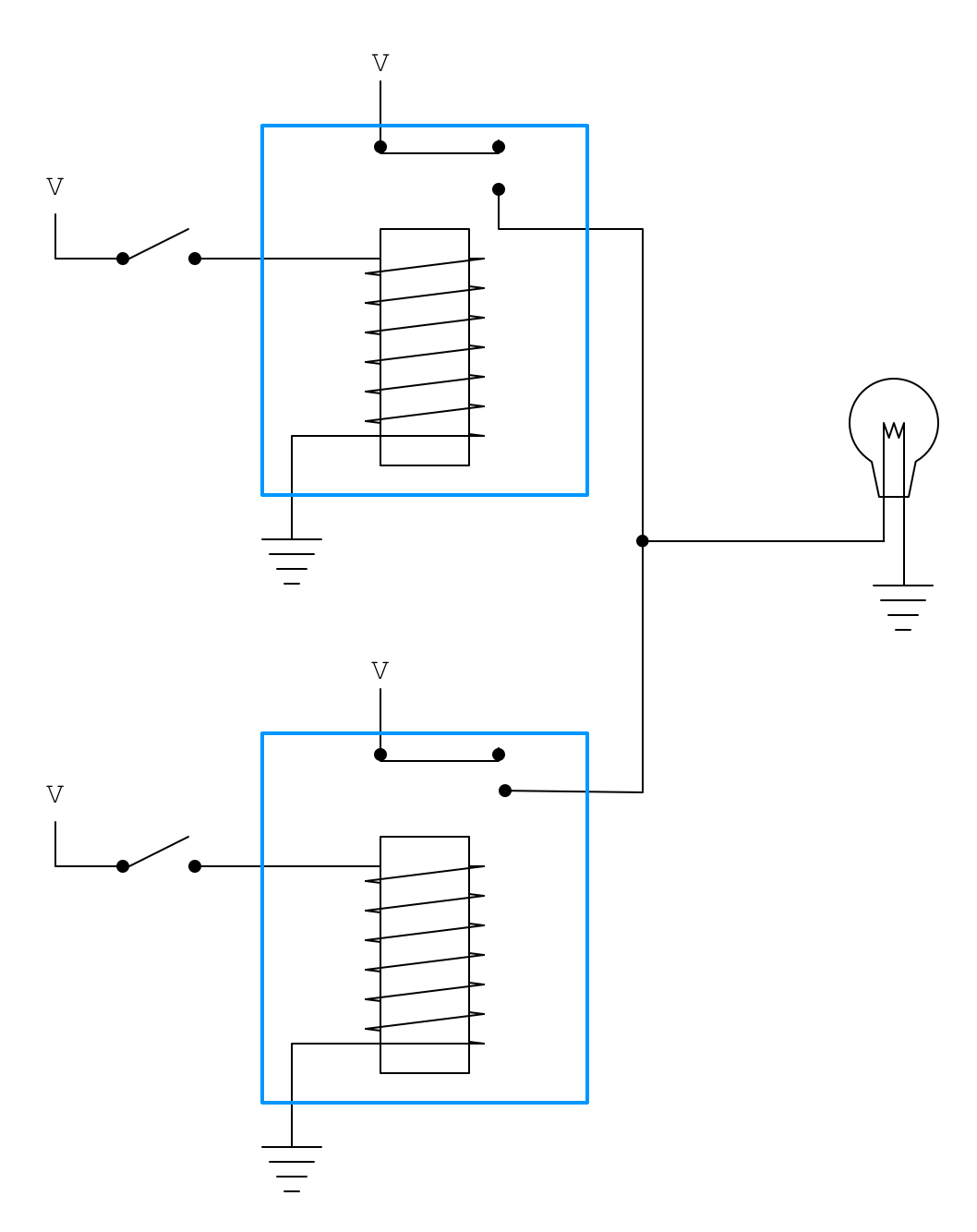
或门可以简记为下面的符号：

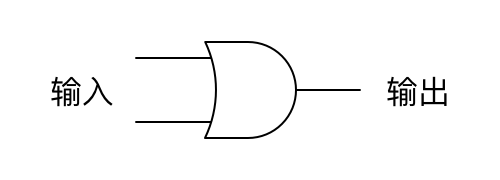
类似地，如果用 0 表示线路断开，1 表示线路连接，那么或门的输出与输出之间的关系如下：

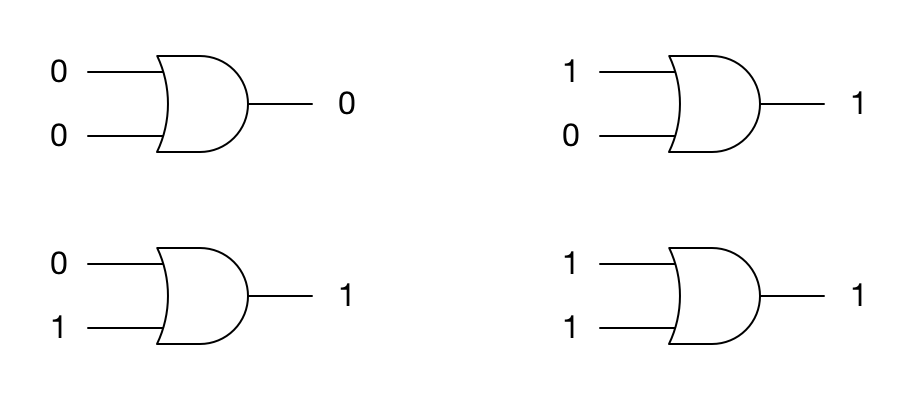
或者总结为一个表格：

OR	0	1
0	0	1
1	1	1

非门

前面的继电器线路中，输出线路与输入线路是一致的，即输入线路的开关接通，输出线路也接通，输入线路断开，输出线路也断开。但其实，我们完全可以做一个小改造，让两者的行为反过来。如下图：

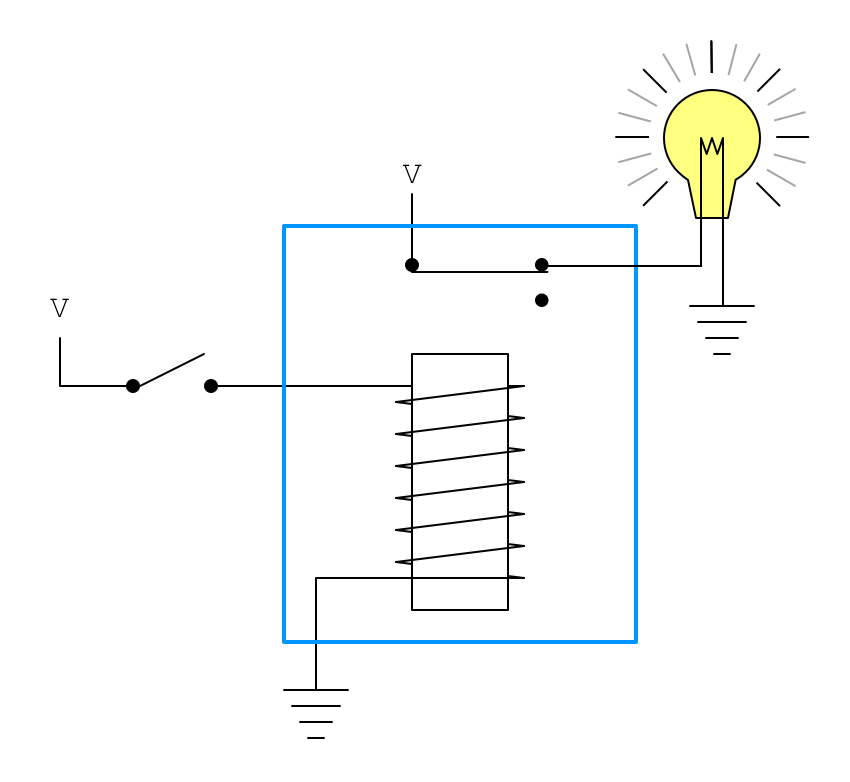
上面的电路图中，左边的开关打开时，右边的灯泡会亮，左边的开关闭合时，右边的灯泡会熄灭，行为正好与控制开关相反。用这种方式连接的继电器叫反向器，或者叫非门。可以用以下符号表示：

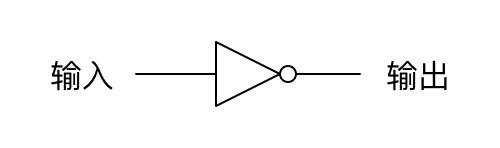
异或门

与门、或门、非门是三种最基础的门，所有其他逻辑运算都可以由这三种门组合得到。不过，为了方便起见，有一些常用的组合也有专门的名字，比如异或门（XOR）。

异或门结构如下：

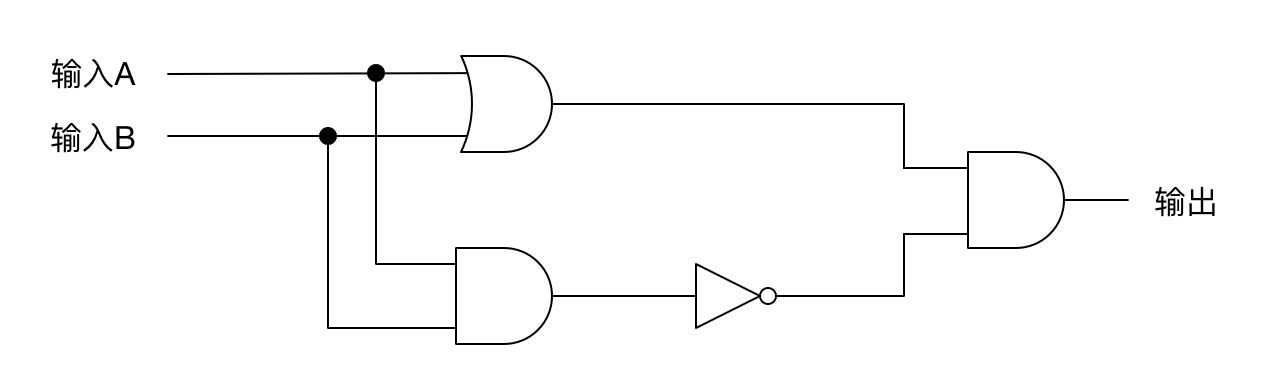
可简记为以下符号：

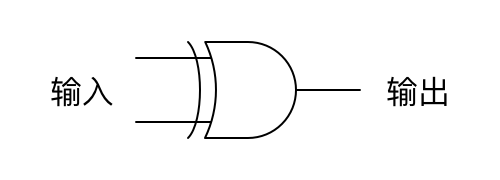
异或门的输入输出可表述为下表：

XOR	0	1
0	0	1
1	1	0

4、二进制加法器

二进制的加法表非常简单，一共只有4种情况：

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10

也可以用表格表示：

+	0	1
0	00	01
1	01	10

注意到 1 + 1 时产生了进位，我们可以把加法表拆成两个表，一个表只记录当前位：

+当前位	0	1
0	0	1
1	1	0

一个表只记录进位：

+进位	0	1
0	0	0
1	0	1

对照上面的各个门，可以发现，进位表对应与门（AND），当前位表则对应异或门（XOR）。

有了上面的基础，我们就可以开始实现二进制的加法器了。首先实现的是两个二进制一位数的加法器：

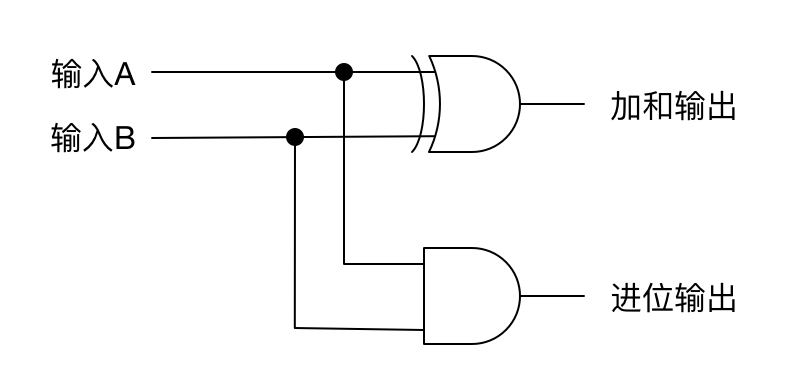
这个装置称为半加器，可以简记如下：

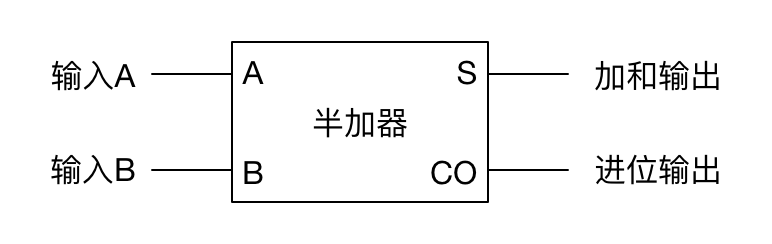
它之所以叫半加器，是因为它只能处理两个数字（二进制一位数）的相加，不能处理前面计算的进位。为了处理进位，可以将两个半加器和一个或门连接如下：

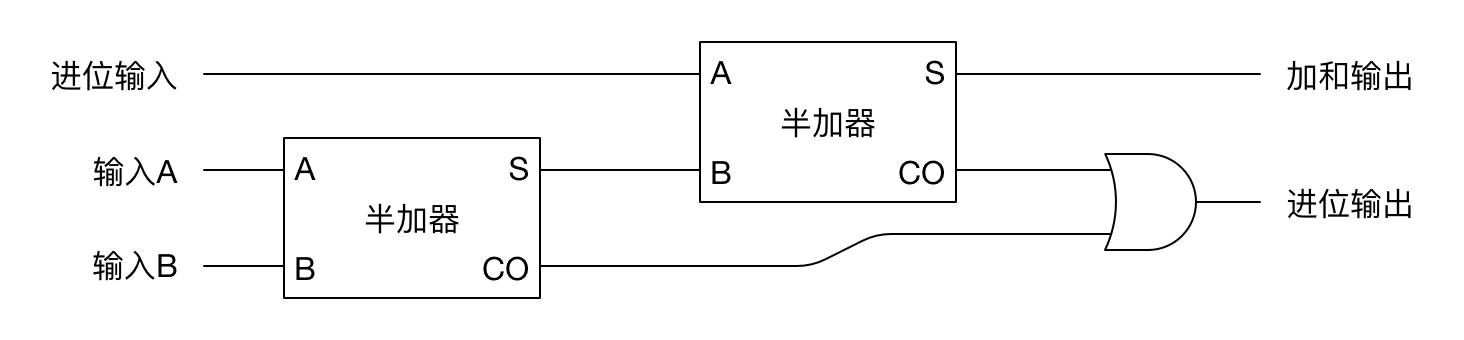
或者简记如下：

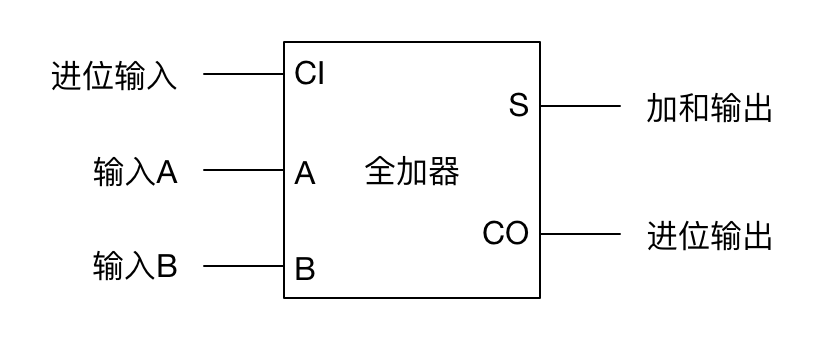
一个全加器只能处理三个二进制一位数（其中一位是进位输入）的相加。如果要处理多位数的相加，需要将多个全加器连接起来。

下面是一个 8 位二进制加法器的连接方法：

第 1 个全加器：

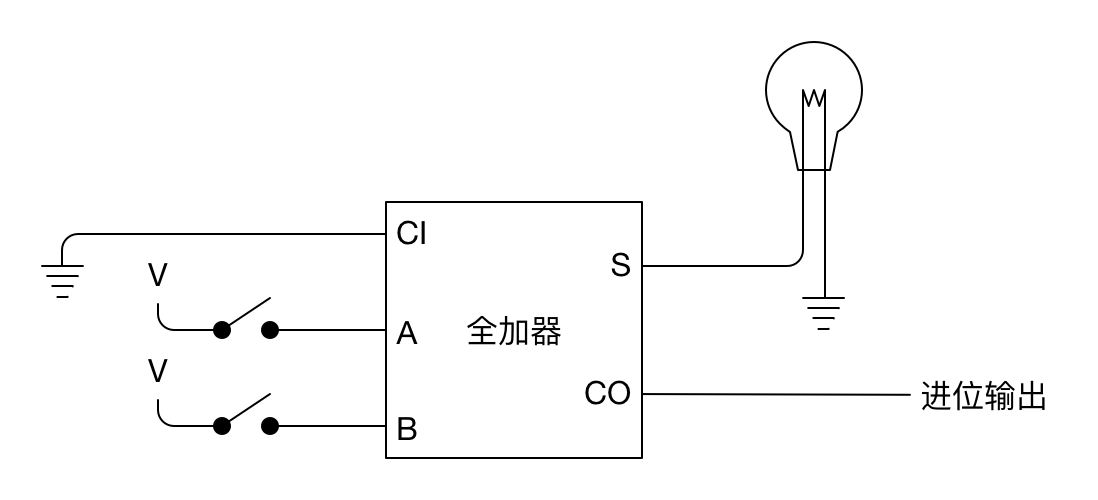
第 2～7 个全加器：

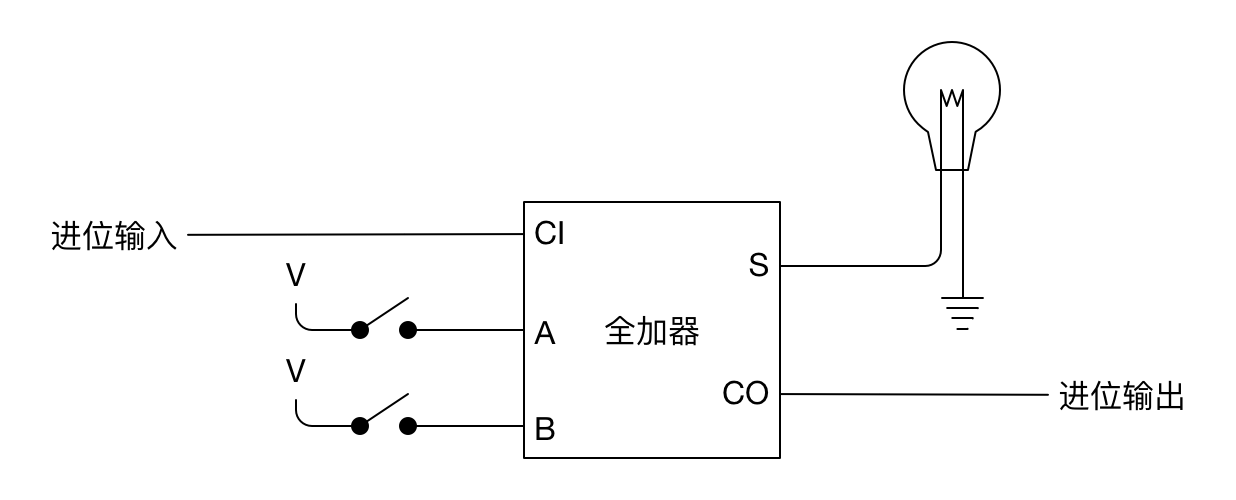
第 8 个全加器：

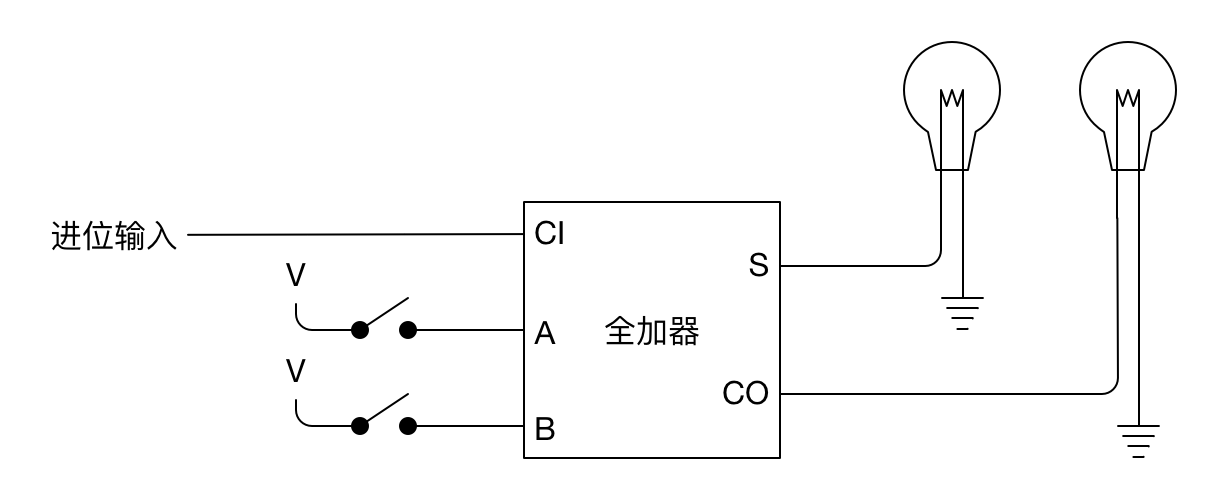
完整线路图如下所示：

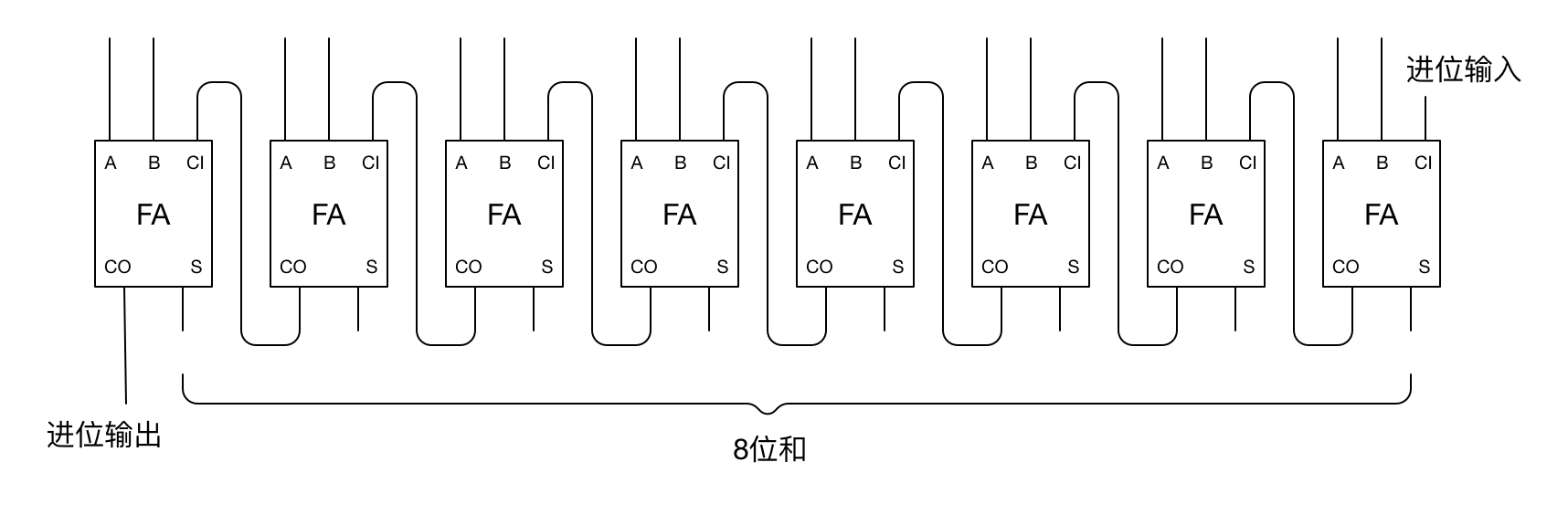
以上就是二进制加法器的原理。