竞争市场上商家收入与其排名之间的关系
说明:这篇帖子是 2006 年写的,数据也是 2006 年的。
前几日看到移动百宝箱 7 月 KJAVA 全网排名前 20 名的当月收入表格,隐约觉得其中会有关系可挖掘,便将其按收入从高到低排列,画出柱状图,再添加趋势线,发现收入 y 与排名 x 之间有非常完美的指数函数关系,如下图所示:
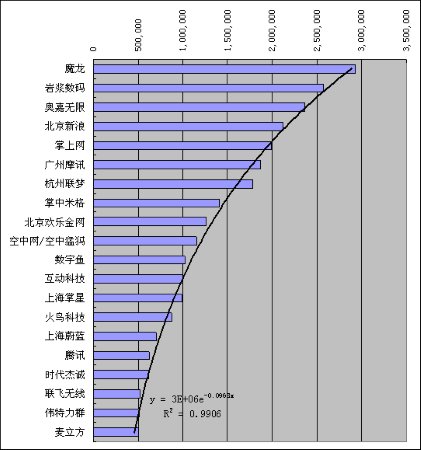
其中 \(y\) 与 \(x\) 的关系为:
\[y = 3E+06 * e^{-0.0968x}\]
于是,设第 \(t\) 名的收入为 \(f(t)\) ,则有:
\[f(t) = ae^{-bt} \text{,其中a = 3E+06,b = -0.0968}\]
这是一个指数函数,设 \(F\) 为 \(f\) 的原函数,有:
\[F(x)=\int_{0}^{x} ae^{-bt}dt\]
这儿 \(F(x)\) 是 \(f(t)\) 的变上限积分,其意义为前 \(x\) 名商家的业务总和,计算,有:
\[F(x) = \frac{a(1 – e ^ {-bx})}{b} \tag{1}\]
由 (1) 式,我们可以得到以下信息:
- \(F(+∞) = \frac{a}{b} = \frac{3E+06}{0.0968} = 30991735.54\),意义:目前这个市场的总体规模为 3000 万元;
- \(\frac{F(20)}{F(+∞)} = 0.8557\), 意义:前 20 位商家占了 85.57% 的市场份额;
- \(\frac{F(7.16)}{F(+∞)} = 0.5\), 意义:前 8 位商家占了 50% 以上的市场份额。
以上只是粗略计算,仅供参考,如果能得到更多的数据相信能做出更精确、更准确的分析与判断。
非常有趣,在一个竞争的市场上前 N 位商家的收入与它的排名竟然有这样一个简单的关系,由此我们可以在知道了前 N 位商家收入的情况下估算出市场总额。相信,如果这个市场足够大并且竞争足够(理想条件下),收入与排名之间的关系应该充分符合指数函数的关系的。
想起去年时我做的另一个统计:统计一个下载网站的下载记录,将所有下载软件按某一段时间内的下载量从高往低排列,并画出散点图,结果图表看起来如下:
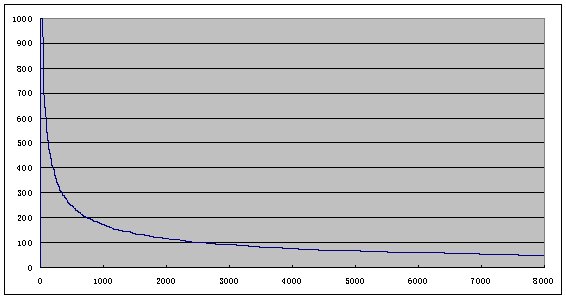
其中横轴为软件的下载排名 \(x\),纵轴为软件的下载量 \(y\),结果发现 \(y\) 与 \(x\) 之间有这样的关系:
\[y = ax^{-b} \text{ ,其中 a>0, b>0} \tag{2}\]
与竞争市场上收入与排名之间的关系不同,这儿的关系是幂函数关系。
当时曾在网络上搜索过,发现一个类似的定理:Zipf 定理。Zipf 定理的内容大致是:将人类语言中的词汇按使用频率由高到低排列,则使用频率 \(y\) 与排名 \(x\) 之间有这样的关系:
\[y \propto \frac{1}{x}\]
仔细看我上面下载图表 (2) 式中 \(y\) 与 \(x\) 的关系,再来看 Zipf 定理,会发现 Zipf 定理是下载图表 (2) 式关系中当 \(b = 1\) 时的特例。另外,根据当时网站上百万条下载记录统计出来的数据则显示下载图表关系中的 \(b < 1\)。
上面的下载图表关系应该也是一个普遍存在的关系,表示人们对事物的喜好程序的一种关系,何时 \(b = 1\),何时 \(b ≠ 1\)呢?如果有,会发生在什么事物上呢?我现在还不知道。
评论: