一些数学作业中，经常有给定一个数列的前几项，让你寻找规律，填写下一项的问题。比如这样：

请填写数列的下一项：1, 3, 5, 7, ____

这种题目一般不会太难，比如上面这题，我们可以合理地推测这是一个等差数列，因此下一项是 9。

回答这类题目的时候，我们心中通常会有一些默认的假设，比如假设题目不会太超纲，数列的规律也不会太复杂，不然的话，这类题目恐怕就没法简单地回答了。

问题

前几日，我在网络上看到一个图片，就对上面的题目给出了一个有点搞笑却又有理有据的回答：

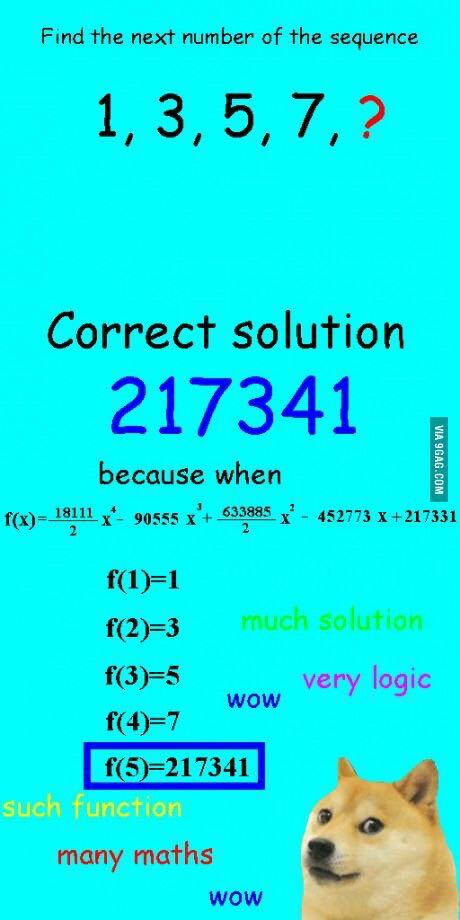
作者说，数列 1, 3, 5, 7 的下一项是 217341，因为这个数列的规律（通项公式）是：

\[f(x)=\frac{18111}{2}x^{4}-90555x^{3}+\frac{633885}{2}x^{2}-452773x+217331\]

我写代码验证了一下，这个公式是正确的，如下：

const f = (x) => 18111/2 * Math.pow(x, 4) 
		- 90555 * Math.pow(x, 3) 
		+ 633885/2 * x * x 
		- 452773 * x 
		+ 217331

console.log(f(1))
console.log(f(2))
console.log(f(3))
console.log(f(4))
console.log(f(5))

执行，输出结果为：

1
3
5
7
217341

所以说，数列 1, 3, 5, 7 的下一项，完全可以不是 9，而是一个奇怪而复杂的数字。

笑过之后，我不禁在想，这个通项公式是怎么得到的呢？还有其他函数有这样的效果吗？

探索

一番思考之后，我发现答案其实很简单，如果把数列的序号以及值看做坐标变量 x、y，那么这其实就是给定几个散点，求一条拟合曲线的问题，这样的公式完全可以根据需要算出来，而且有无穷多个。

就以上面的公式为例，可以看到，它是一个一元四次多项式，如果我们把 \(\frac{18111}{2}\) 这样的常量用字母来代替的话，这个函数可以写成下面的一般形式：

\[f(x)=ax^{4}+bx^{3}+cx^{2}+dx+e\]

然后，根据已知数列，我们有：

\[ \begin{split} f(1) &= a + b + c + d + e = 1\\ f(2) &= 16a + 8b + 4c + 2d + e = 3\\ f(3) &= 81a + 27b + 9c + 3d + e = 5\\ f(4) &= 256a + 64b + 16c + 4d + e = 7\\ f(5) &= 625a + 125b + 25c + 5d + e = ? \end{split} \]

也即：

\[ \begin{equation} \left\{ \begin{split} &a + b + c + d + e = 1\\ &16a + 8b + 4c + 2d + e = 3\\ &81a + 27b + 9c + 3d + e = 5\\ &256a + 64b + 16c + 4d + e = 7\\ &625a + 125b + 25c + 5d + e = ? \end{split} \right. \end{equation} \]

这是一个很普通的五元一次方程组，其中第五个等式的值即是数列第 5 项 \(f(5)\) 的值。

在我们最初的解答中有 \(f(5)=9\)，将其代入方程组，可以解得：

\[a=0,b=0,c=0,d=2,e=-1\]

即：

\[f(x)=2x-1\]

可以看到，这就是一个简单的等差数列。

在这个五元一次方程组的基础上，我们可以继续前进，比如构造出一个公式，让数列的前四项是 1, 3, 5, 7，而第五项是任意我们想要的值。今年是 2020 年，就让我们来构造一个让数列的第五项是 2020 的公式吧，操作很简单，将方程组第五个等式右侧的问号换成 2020 即可：

\[ \begin{equation} \left\{ \begin{split} &a + b + c + d + e = 1\\ &16a + 8b + 4c + 2d + e = 3\\ &81a + 27b + 9c + 3d + e = 5\\ &256a + 64b + 16c + 4d + e = 7\\ &625a + 125b + 25c + 5d + e = 2020 \end{split} \right. \end{equation} \]

解之，得：

\[a=\frac{2011}{24}, b=-\frac{10055}{12}, c=\frac{70385}{24}, d=-\frac{50251}{12}, e=2010\]

即：

\[f(x)=\frac{2011}{24}x^{4}-\frac{10055}{12}x^{3}+\frac{70385}{24}x^2-\frac{50251}{12}x+2010\]

你可以验证一下，在这个公式下，\(f(x)\) 的前五项值分别为：1, 3, 5, 7, 2020。

甚至，你也可以构造出这样的公式：

\[f(x)=\frac{10288065}{2}x^{4}-51440325x^{3}+\frac{360082275}{2}x^2-257201623x+123456779\]

在这个公式下，数列的前五项将是：1, 3, 5, 7, 123456789 。

也就是说，你想让第五项等于几都行，可以是 -1、233333333、π、\(\sqrt{2}\)，甚至还可以是虚数，你所要做的，就是将想得到的数字代入上面的五元一次方程组，解出这个方程，从而得到通项公式 \(f(x)\) 各项的参数。

这儿为了简单起见，\(f(x)\) 函数中使用的是多项式，如果你想弄得复杂点，\(f(x)\) 中也可以使用指数函数、三角函数等等。当然，弄得太复杂的话可能会很难解出方程中常数的值来，如果你只是想凑一个公式，让数列的下一项得到任意指定的值，那么多项式就足够了。

另外，任意长度的数列找规律都可以使用这个方法，原因上面说了，这本质上就是一个给定若干散点求拟合函数的问题，使用拉格朗日插值法等方法，总是能找到符合要求的多项式函数。

小结

下次再看到数列找规律的题目，你就知道啦，从理论上来说，你完全可以任意填写一个数字，比如你的生日，然后给老师看这篇文章，告诉老师你可以给出对应的通项公式来。当然，如果你真的这么做，你有很大的概率会被扣分，所以正式考试的时候还是按题意来回答吧。

最后，关于这个数列的问题，我也做了一个在线演示，你可以在其中随意填写数字，并生成对应的通项公式，欢迎点击试玩。