关于乱停车的概率题
听闻我厂新厂区发生了若干次乱停车的问题,某些同学占了别人的车位,导致车位的主人无法正常停车。在这儿,我们抛开孰是孰非的评论,仅从数学的角度来考察一下这个问题,如果一位同学随便停车,可能会影响到多少人呢?
问题
为了方便讨论,让我们把问题重新定义一下:
设厂区有 n 个车位,对应的也有 n 位开车的同学,每位同学有一个专属的车位,车位与同学之间是一一对应的关系。假设最先到的 1 名同学没有遵守停车规则,他没有刻意去寻找自己的车位,而是随机选了一个位置停车(注意,这儿说的是随机,也就是这位同学也有一定的概率将车停到自己的位置上),后来的同学如果发现自己的车位没有被占,则将车停在自己的车位上,如果发现自己的车位被占了,则也在剩下的车位里随机选择一个停放。我们的问题是,从期望上来说,最后会有多少人停错位置?
分析
为了便于分析,我们假设前 q 名同学(1⩽q⩽n)都不遵守规则,选择随机停车。很容易可以看到,前 q 名随机停车的同学,正好停到自己的位置上的概率为 \(\frac{1}{n}\),则他们停错的概率为 \(1- \frac{1}{n}\),即 \(\frac{n-1}{n}\) 。
我们用 F(i) 来表示第 i 名同学停错的概率,则有:
\[F(i)=\frac{n-1}{n}, (1 \leq n \leq q)\]
从第 q+1 名同学开始,他们会优先停在自己的车位上,仅当自己的车位被占时才随机停车,所以他们停错位置的概率即是他们的位置被前面的车占了的概率。可以发现,第 q+1 名同学的车位被占的概率(车位被前 q 名随机停车的同学占的概率)为 q/n ,这也是他自己停错位置的概率。即:
\[F(i)=\frac{q}{n}, (i = q + 1)\]
继续分析,可知第 i 名同学停错车的概率(他的车位被前 i-1 名同学占了的概率)为:他的车位被第 1 名同学占了的概率 + 他的车位被第 2 名同学占了的概率 + ... + 他的车位被第 i-1 名同学占了的概率。
因此,考察第 q+2 名同学,他的车位被前 q 名同学占了的概率为 q/n,即我们只需要求出他的车位被第 q+1 名同学占了的概率即可。而第 q+1 名同学要占他的车位,说明第 q+1 名同学的车位也被前面的同学占了,他只能在剩下的车位同随机停放。于是,我们可以得到下面的算式:
\[F(i=q+2)=\frac{q}{n} + F(i-1)G(i)\cdot \frac{1}{n-i+2}\]
其中 G(i) 的含义是:在第 i-2 名同学发现自己的车位被占的情况下,第 i-1 个车位仍然空着的概率。因为只有这种情况下,第 i-1 个位置才有可能被 第 i-2 名同学占用。(n-i+2) 表示当第 i 位第 i-1 位同学准备停车但还没有停时剩下的空位置数量。
接着,我们又可以推出 F(q+3):
\[F(i=q+3)=\frac{q}{n}+F(i-2)G(i-2)\cdot \frac{1}{n-i+3}+F(i-1)G(i-1)\cdot \frac{1}{n-i+2}\]
观察上式右边,可以注意到它的前面的几项正好等于 F(q+2),即:
\[F(i=q+3)=F(i-1)\cdot(1+G(i-1)\cdot\frac{1}{n-i+2})\]
接着,我们可以推出 F(i) 的通用公式,这是一个分段函数:
\[F(i)=\begin{cases} \frac{n-1}{n}, (1 \leq i \leq q)\\ \frac{q}{n}, (i = q + 1)\\ F(i-1)\cdot (1+G(i-1)\cdot \frac{1}{n-i+2}), (i>q+1)\\ \end{cases} \]
好吧,看起来有点复杂,而且函数 G(i) 还没有展开。不过幸运的是,如果我们只考虑 q=1 的情况,我们马上能发现 G(i) 总是等于 1,因为只有一名同学随机停车,当他占了别人的车位时,就换成那名车位被占的同学开始随机停车,无论如何,当某位同学发现自己的车位被别人占了时,还没来的同学的车位一定都还是空的,没有被其他人占用。
这样一来,我们的公式就变成了:
\[F(i)=\begin{cases} \frac{n-1}{n}, (i = 1)\\ \frac{1}{n}, (i = 2)\\ F(i-1)\cdot (1+ \frac{1}{n-i+2}), (i>2)\\ \end{cases} \]
其中 i>2 的情况可以继续化简:
\[ \begin {aligned} F(i)\\ &=F(i-1)\cdot \frac{n-i+3}{n-i+2} \\ &=\frac{1}{n}\cdot\frac{n}{n-1}\cdot\frac{n-1}{n-2}\cdot\frac{n-2}{n-3}\cdot \cdot\cdot\cdot \cdot\frac{n-i+4}{n-i+3}\cdot\frac{n-i+3}{n-i+2} \\ &=\frac{1}{n-i+2} \end {aligned} \]
再注意到当 i=2 时,上式正好等于 \(\frac{1}{n}\),即:
\[ F(i)=\begin{cases} \frac{n-1}{n}, (i=1) \\ \frac{1}{n-i+2}, (i \geq 2) \\ \end{cases} \]
这样,我们便得到了当第 1 位同学随机停车时,各位同学停错车位的概率,或者说停错车位的期望值。接着,我们将这 n 位同学停错车位的期望值加起来,就得到了总的期望,设为 S(n) ,则有:
\[S(n)=\sum_{i=1}^n{F(i)}\]
这个函数如果画出一个图形来,是这个样子的:
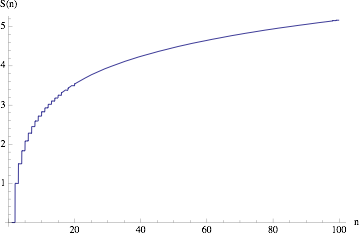
其中 n 的值为 1、2、3... 这样的自然数,这也是函数图像上出现“锯齿”的原因。
结论
从上面的公式及图形上,我们很容易计算出在不同的总车位下(即 n 不同时),第一名同学乱停车会导致多少人停错位置的期望值。
我们来看一个具体一点的数字,比如 n=100,计算可知 S(100) 约为 5.18。也就是说:
如果厂区某个区域有 100 个车位及对应的同学,第 1 位同学随机停车,接下来的同学如果自己的车位没被占就停自己的车位,被占了就在剩下的位置中随机选一个停车,如果这样的试验重复多次,那么平均下来每次约有 5.18 名同学会停错车位(包括第 1 位随机停车的同学)。
更多
网上有一些类似问题的讨论,比如搜索“傻子坐飞机问题”,即可找到一个类似的问题,不过那个问题更关注的是最后一名同学仍然能坐对自己的位置的概率,而不需要知道中间的同学坐对或坐错的概率。另外,《编程之美》一书中有一个“金刚坐飞机问题”也与本题非常类似。
上面 S(x) 的函数图像可以用一个对数函数的图像来拟合,误差非常小,如下图:
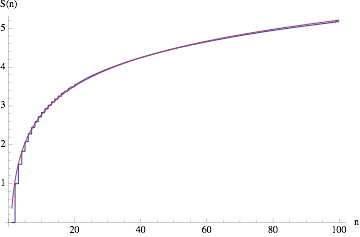
其中那条红线的方程是:\(f(x) = 1.0534 * \ln(x) + 0.3557\)。
评论:
(n-i+2) 表示当第 i 位同学准备停车但还没有停时剩下的空位置数量? 为什么不是n-i+1?
那儿应该是“第 i-1 位”同学,笔误,已更正。看得真仔细!:)
G(i) 的含义是:在第 i-2 名同学发现自己的车位被占的情况下,第 i-1 个车位仍然空着的概率。这句话我也不是很懂,我觉得G(i)的含义是:在第 i-2 名同学发现自己的车位被占的情况下,第 i 个车位仍然空着的概率。
我理解错了。但是我觉得
F(i=q+2)=n/q + F(i-1)*G(i-1)*1/(n-i+2) 而不是F(i=q+2)=n/q + F(i-1)*G(i)*1/(n-i+2) 。
因为,你后面的公式 G和F的参数都是同一个数。。。。。
结尾的居然是magic number差评……