网格路径问题
题目是这样的:
Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner.
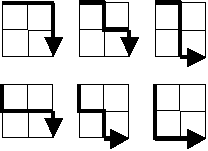
How many such routes are there through a 20×20 grid?
这个题来自 Project Euler 的第 15 题。翻译为中文的话,题意大致是:
从一个 2x2 的网络的左上角出发,只能向右或向下移动,到右下角一共有 6 种不同的走法。那么,对一个 20x20 的网络来说,有多少种不同的走法呢?
我们来绘制一个大一些的网格,并将它的横向记为 X 坐标,纵向记为 Y 坐标,每个交点依次编号,如下图:
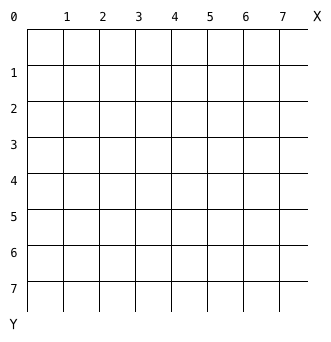
这样,我们都可以使用形如 (x, y) 这样的坐标来表示网格中的每一个交点了,比如下图中的黑点位置可以用坐标 (4, 3) 来表示。
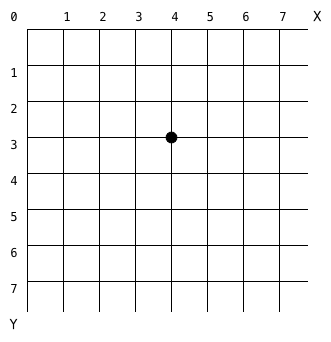
可以发现,如果从左上角即坐标 (0, 0) 处出发,只能向右或向下移动,到达接下来几个交点的走法类似下图所示:
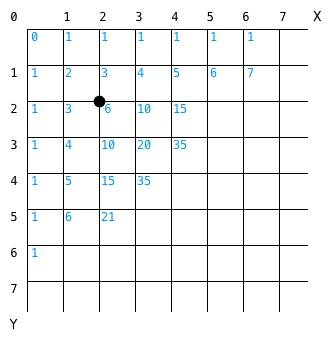
每个交点右下方的蓝色数字表示从左上角出发到达这个位置的不同走法,例如坐标 (2, 2) 右下角的数字是 6 ,即到达这个位置共有 6 种不同的走法。这也即原题中 2x2 的格子的不同走法。
观察这个网格,可以发现除了最上边及最左边的交点外,各个交点的走法等于它上方及左方交点走法的和。
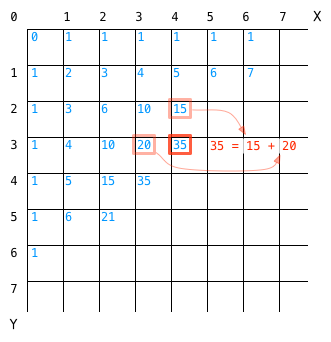
如上图所示,坐标 (4, 3) 处的走法共有 35 种,等于它上方的网格 (4, 2) 的走法(15 种)加上它左方的网格 (3, 3) 的走法(20 种)之和。
也就是说,如果用函数 r(x, y) 来表示到达坐标 (x, y) 的走法,我们可以总结出下面的公式:
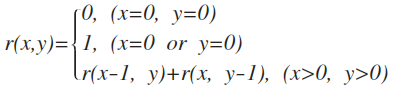
根据上面的公式,我们很容易编写出对应的代码来,以 Python 为例:
def r(x, y):
if x == 0 and y == 0:
p = 0
elif x == 0 or y == 0:
p = 1
else:
p = r(x - 1, y) + r(x, y - 1)
return p
不过,需要注意的是,上面的代码用到了递归,当 x、y 的值变大时,递归的次数以指数级别上升,因此,要计算 r(20, 20) ,用这个方法效率是非常低的。我们可以再将程序改进一下,像下面这样:
def r(x, y):
d = []
for i in range(y + 1):
t = [0] * (x + 1)
d.append(t)
for iy in range(y + 1):
for ix in range(x + 1):
if ix == 0 and iy == 0:
v = 0
elif ix == 0 or iy == 0:
v = 1
else:
v = d[iy - 1][ix] + d[iy][ix - 1]
d[iy][ix] = v
return d[y][x]
这样便快很多了,很容易计算出,r(20, 20) 的值为 137846528820,也即对一个 20x20 的网格来说,从左上角走到右下角,一共有 137846528820 种不同的走法。
至此,这题便解答完成了,在 Project Euler 的论坛上还有很多种其他解法。另外,观察这个网格,每个交点处的值都是它上方及左方两个交点的值的和,这一点有点像斐波那契数列,不过形式上是二维的。
评论:
老杰……咱俩博客主题居然是一个……你刚换主题了?……
哈哈,是刚换,感觉这个主题比自带的好看多了。:D
不懂python, 问下改进版的第2,4行表示什么意思?
第2~5行是为了生成一个宽度为 x+1,高度为 y+1 的二维数组,用来表示那个网格。
其中第2行是定义一个新的空数组,第4行是为这个数组追加一行内容(一个长度为 x+1 ,值全为 0 的一维数组)。
//C++.动态创建二维数组真不方便
#include
using namespace std;
unsigned long long r1 (size_t x, size_t y)
{
unsigned long long p;
if (x == 0 && y == 0)
p = 0;
else if (x == 0 || y == 0)
p = 1;
else
p = r1(x - 1, y) + r1(x, y - 1);
}
unsigned long long r2 (const size_t x, const size_t y)
{
unsigned long long* p = new unsigned long long[(x+1)(y+1)];
for (size_t i = 0; i <= x; ++i)
p[i(y+1)+0] = 1;
for (size_t i = 0; i <= y; ++i)
p[0*(y+1)+i] = 1;
for (size_t ix = 1; ix <= x; ++ix)
for (size_t iy = 1; iy <= y; ++iy){
p[ix*(y+1)+iy] = p[(ix-1)(y+1)+iy] + p[ix(y+1)+(iy-1)];
}
size_t line = 0;
for (size_t a = 0; a < (x+1)(y+1); ++ a){
cout << p[a] << "t";
if (!(++line % (y+1)))
cout << endl;
}
unsigned long long ret = p[x(y+1)+y];
delete p;
return ret;
}
int main(int argc, char const *argv[])
{
cout << r2(30,30);
return 0;
}
赞~
老杰,你好。请教一下,你现在使用的主题怎么让首页和归档也显示摘要的呢?
这个主题有这个选项啊,在 外观 -> Contango Theme Settings -> Posts settings 里,Post Style 一项选 Excerpt 就可以了。
之前没看到,呵呵。这么简单!!
有点深度,得慢慢消化
对于 m×n 的格子,答案是 (m+n)! / m!n! 好像?
啊,进论坛看了,就是40选20啊,第一页最后一个 post……
杨辉三角
犀利~
最近刚写过 http://weibo.com/1408056531/Cl0M7jFBE 菜鸟初学 :D
其实可以快速求的,O(n)预处理,log(n)求单点的值(取模)。