写了一段寻找质数的 Python 脚本玩，断断续续跑了两三天，终于把 1 亿以内的质数全找出来了，并将它们从小到大排列保存为了文本文档，与我一样无聊且又不想自己算的朋友可以右键点击这儿另存为（12.5M）下载下去玩玩。

然后又写了一个脚本统计了一下每 n 个连续的自然数中质数出现数量的变化，当 n=100000 时，得到下图：

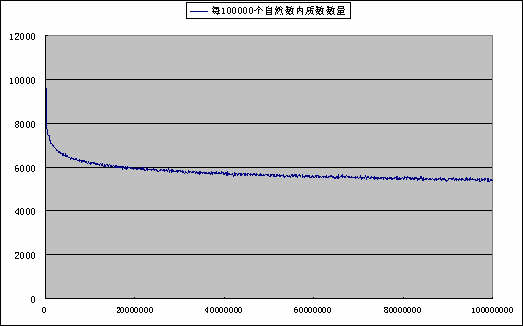
可以看到，在 0～100000 间共有 9592 个质数，在 100001～200000 间共有 8392 个质数，...而在 99900001～100000000 间则只有 5454 个质数了，随着数字的增大，质数越来越稀少。

不过，尽管从直观上与经验上可以得出随着数字的增大质数的出现概率越来越小的印象，这个概率却并不会减至 0，即不存在最大的质数。关于这个结论，几千年前欧几里德就已经巧妙地证明，他的证明如下：

假设只有有限个质数，如 n 个：\(2, 3, 5, ..., p\)，则可以构造一个数 \(M = 2·3·5·...·p + 1\)。\(M\) 如果是合数，则必有一个质数因子 \(q\)，因为只有有限个质数，所以 \(q\) 必然是 \(2, 3, 5, ..., p\) 中一个。但是 \(q\) 必然不同于 \(2, 3, 5, ..., p\) 中任意一个，因为用 \(2, 3, 5, ..., p\) 中的任何一个去除 \(M\) 总是会余 \(1\)。因此，质数有无穷多个。

质数是有无穷多个的，华裔青年数学家陶哲轩和他的同事则进一步证明了另一个结论：质数存在任意长的等差数列。比如，3, 7, 11 三个质数即是一个差为 4 长度为 3 的等差数列，陶及他的同事的研究揭示，在质数排列的某个地方，在在一个长度达 1001000 或其他任意有限值的序列，这些序列的数量是无限的。

上网搜索了一下，目前人类找到的最大的质数似乎是这个：\(2^{30402457} - 1\)，在 2005 年 12 月由美国密苏里州立大学的 Curtis Cooper 和 Steven Bonne 发现，长度达到惊人的 9152052 位，是第 43 个梅森质数（梅森质数指形如 \(2^n-1\) 的质数，以 17 世纪法国著名数学家、法兰西科学院奠基人梅森命名），被记作为 M30402457 ，据说这个质数是花了多年时间给 700 部电脑进行编程之后才被发现。

以下关于梅森质数的描述摘自 http://www.mathren.com/n162c12.aspx：

梅森素数貌似简单，但研究难度却很大。它不仅需要高深的理论和纯熟的技巧，而且需要进行艰巨的计算。 1772 年，被誉为“数学英雄”的欧拉在双目失明的情况下，以惊人的毅力靠心算证明了 \(2^{31}-1\) 是第 8 个梅森素数，该素数有 10 位数，堪称当时世界上已知的最大素数。1963 年 9 月 6 日晚上 8 点，当第 23 个梅森素数 \(2^{11213}-1\) 通过大型计算机发现时，美国广播公司（ABC）中断了正常的节目播放，以第一时间发布了这一重要消息；而发现这一素数的美国伊利诺伊大学数学系全体师生感到无比骄傲，以致于把所有从系里发出的信件都盖上了“\(2^{11213}-1\) 是个素数”的邮戳。特别值得一提的是，中国数学家和语言学家周海中经过多年的研究，于 1992 年首先给出了梅森素数分布的准确表达式，为人们探寻梅森素数提供了方便；后来这一成果被国际上命名为“周氏猜测”。

其他：

除了寻找质数，用计算机来寻找圆周率 π 也很好玩，非常适合于无聊时用来折腾电脑以及消磨时间。以前我曾在计算机上模拟纸笔运算来计算π，但算法不够好，算得比较慢，而且后来发现当我想算到 10 亿位或 100 亿位以上之时，最大的瓶颈居然是我电脑的硬盘空间不够（谁叫我当时那么穷买不起更大的硬盘呢？），毕竟 10 亿位数字就是 1G 的空间，除此之外，计算的中间过程也需要很多的硬盘开销。