关于页面停留时间
页面停留时间(Time on Page)是网站分析中的一个重要指标,用于反映用户在某个(或某些)页面上停留时间的长短。
如果我们把用户到达本页面的时间记为 t0,那么计算用户在页面上的停留时间主要有两种方法:
- 离开时记录:用户离开本页面的时间
t1减去t0; - 到达下一个页面时记录:用户到达下一个页面的时间
t2减去t0。
两种方法都有缺点,其中第一种方法需要监听页面的onbeforeunload事件,在事件触发时发送一个打点,但这个打点有一定的丢失率。第二种方法是目前比较通用的方法,包括Google Analytics在内的很多系统都使用这个方法,但是它会丢掉用户在访问路径中最后一个页面上的停留时间。
不过,本文的重点并不是讨论如何记录这个时间。现在,姑且假定我们已经取得了所有PV的页面停留时间了,下一步我们应该如何处理呢?
一、问题
我们来看一组真实的数据:
2.735
20.859
480.924
16.031
70.682
11.672
11.625
8.422
25.156
16.640
28.703
50.172
22.500
32.968
33.859
890.730
8.801
2207.547
...
上面的每一行代表某次PV在页面上的停留时间,单位为秒。你可以从这儿下载到完整的数据,一共2335条记录。
显然,我们不可能把这些记录全部展示给需求方,他们通常并不想知道每个具体的用户在页面上的停留时间,而是想知道一个有代表性的或汇总的数据,以便能对站点的体验有一个总体的把握。
那么,如何计算这个有代表性的或汇总的数据呢?Google Analytics采用的是求均值:
In order to get an average time on page for a specific page, the total time spent on a page for the selected date range is divided by the number of unique visits to that page.
我们来看一下上面的数据的平均数:
最小值:0.078
最大值:19410.0
平均值:288.0
可以看到,2335条记录中,最小值还不足0.1秒,最大值却接近两万秒,平均值则为288秒,或者说4分48秒。到这儿,我们已经可以交差了,告诉需求方,用户平均会在这个页面上停留4分48秒。
但是,接近5分钟的平均停留时间实在是让人惴惴不安,这是不是说,一位典型用户会在我们的页面上停留接近5分钟呢?我们这个页面上没有视频,也没有游戏,仅仅是一个普通的展示页面,很难想象,在浮躁的互联网上会有这么多人在这个页面上停留那么长时间。哪边出了问题?我们应该相信数字还是相信直觉?
二、分析
再一次的分析结果表示,原始数据是没有问题的。那么,让我们再来看一看这些数据的分布情况,如下图。
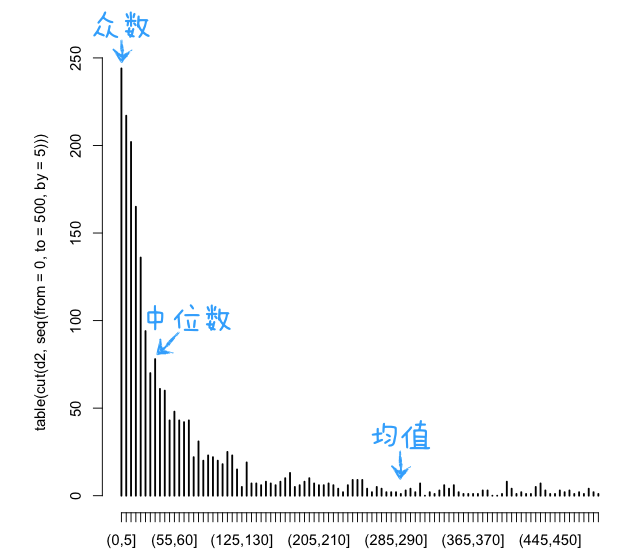
上图只显示了停留时间为0~500秒的记录的分布情况,横轴为用户停留时间,纵轴为出现次数。可以看到,这是一个右偏分布(均值在高峰的右侧),对这种分布来说,总是有均值 > 中位数 > 众数。
从上图可以看到,中位数(一半的数字比它小,一半的数字比它大)其实非常的小,大概只有40秒左右,但是我们得到的均值却高达288秒。这就回答了我们上面的疑问,大部分用户的停留时间其实远小于均值,因此,在这儿均值并不能反映典型用户的访问行为,知道了均值之后我们对大部分用户的停留时间仍然几乎一无所知,假如我们根据这个均值来做决策,则可能会犯下错误(就像在一个贫富严重不均的地区根据平均工资来判断那儿大部分人的购买力一样)。
有些人可能对为什么数据记录中会有一些非常大的值产生疑问,比如真的有人在这个页面上呆了近5个小时吗?答案是确实有这样的情况,比如某个用户可能在打开这个页面之后突然有些其他事要处理,几个小时之后才回来关闭浏览器或访问下一个页面。这种情况可能很罕见,但是它带来的异常值却非常的大,以致于能显著地拉高均值。
同时值得注意的还有左侧有大量的数据在0~5秒之间,也就是说大量用户在网站上的停留时间甚至不足5秒?这也是有可能的,比如有些用户可能在不停地刷新某个页面,或者是由能执行页面上JavaScript脚本的爬虫产生的访问记录。
其实在日常生活中,我们还经常会听到一个量也是类似的右偏分布,即一个公司或地区的平均收入。每当某个统计报告报道了当地的平均收入后,大部分人都会发现自己的收入低于平均收入,于是人们经常质疑统计数据有水份,统计学家们也因此落了个水份最多的名声。但事实上,收入并不是正态分布,而是与上面的页面停留时间类似的一种右偏分布。从这个角度上来讲,如果想用一个数字来了解这种偏态分布的大体状况,中位数可能比均值具有更大的参考价值。
另外,如果我们注意到各条页面停留时间之间是相互独立的,考查对象为指定时间内有多少用户离开页面,那么用户在停留某个时间后离开当前页面的概率大致可以被认为符合泊松分布。
三、探索
从上面的分析我们知道,页面停留时间是一种右偏分布,存在一些非常大的异常值,从而使均值偏向右方。那么,我们是否能先将异常值去掉再计算均值呢?当然是可以的,首先要解决的问题是如何定义异常值?
1
最容易想到的方法是根据经验设定一个阈值,比如30分钟,也即通用的会话过期时间。
用这种方法,我们可以很方便地删除原始数据中大于1800秒的数据,求得剩余部分的均值为134秒。
这种方法得到的结果看起来已经靠谱多了,但还是有一些问题,比如这个30分钟是根据经验得来的,为什么是30分钟而不是10分钟呢?这个数据需要人工指定,如果有些页面上有视频或者游戏,正常情况下的页面停留时间就是要超过30分钟呢?
2
简单来说,我们希望能找到一种算法,能自动删除记录中的异常值,而不需要我们手工指定一个阈值。
在工业界,去除异常值的算法很多,比如信号分析中会用到的滤波算法。另外,如果数据的分布是正态分布的话,还可以用扔掉3倍标准差(σ)以外的数据的方法,因为对正态分布来说,超过99%的数据都会在均值的±3σ之内,如下图所示。
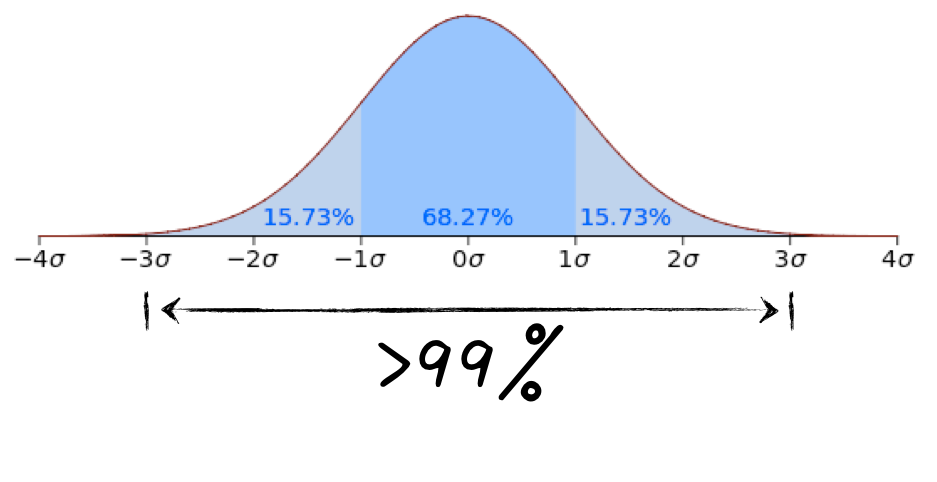
不过遗憾的是,我们上面已经提到,用户停留时间并不是正态分布,因此,使用这种去掉超过3倍标准差的数据的方法效果并不好。
3
看体育比赛时,我们经常会看有很多评委同时打分,最后,裁判会去掉一个最低分和一个最高分,剩下的分数取平均作为运动员的最终得分。注意到,我们的数据中的异常值也基本上要么是太小的数,要么是太大的数,因此,这种朴素的方法在我们这儿其实也可以使用。
当然,我们的数字有成千上万个,我们不可能只去掉一个最小值和一个最大值,而是要批量去掉若干最小值和最大值。一般来说,可以去掉第一个n分位之前和最后一个n分位之后的值。
比如,我们可以将数据从小到大排列,然后按个数平均分成4份(n=4),然后将最前面一份及最后面一份去掉,求剩下部分的均值,如下图所示:
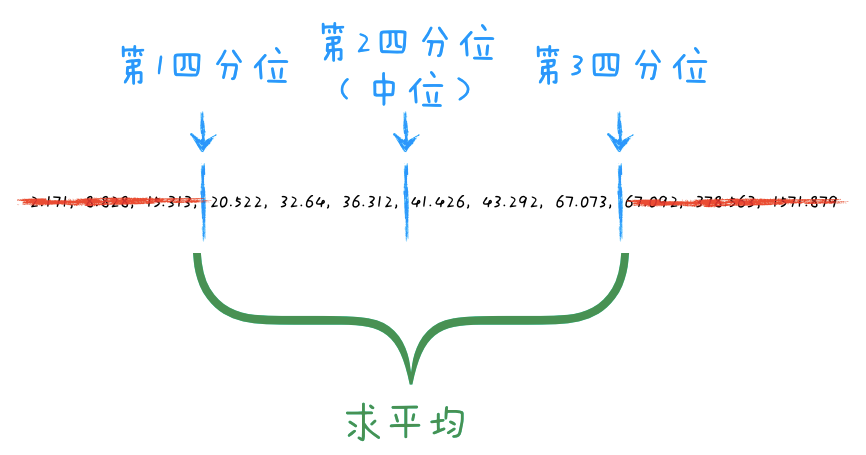
我这儿使用了4分位,当然,你也可以使用5分位、8分位、13分位或其他任何你觉得合适的分位。
对像页面停留时间这样的数据来说这个方法效果不错,最终得到的数据与中位数基本上在一个数量级,而且也比较符合直觉,比简单的求所有数字的平均要更有用一些。
四、小结
网站分析中我们经常会收集到大量的数据,求均值是一种很常见的处理方法,不过,在求均值之前我们也需要注意一下原始数据的分布,如果是正态分布均值通常能很好地反映典型数据的情况,但如果是偏态分布,则可能需要做更多的处理。
评论:
28原则, 只是保留中间的百分之80%呢?
只保留中间的80%其实就相当于方法3中n=10(10分位)的情况,应该也是可以的。
无论分成几份,重要的是选定一个方法后要持续使用,这样才能有持续的可以比较的历史数据,才能看出变化趋势。:-)
对于原始取log,变成类似高斯分布的形式,检验一下是不是符合高斯分布,然后用“扔掉3倍标准差(σ)以外的数据的方法”,留下的数据再返回原始值就成了。这个原始数据中3倍标准差(σ)以外的数值不超过10个,能保留下来的也就1倍标准差(σ)以内的数值。"最终得到的数据与中位数基本上在一个数量级"是说results和results的中位数都在一个数量级?
原始log不符合高斯分布,所以不能用仍掉3倍标准差以外的数据的方法,或者说用了效果不好。
"最终得到的数据与中位数基本上在一个数量级"那个,去头去尾后Q1~Q3的均值是46.123,和中位数37.410很接近,而所有数字的均值达到了288,大了一个数量级。
又没弄明白,请问是用去头去尾后的均值和"原始数据的中位数"37.410比较?这有什么意义么?还是说“去头去尾后”的均值是46.123、中位数是37.410?
“去头去尾后”的均值是46.123、中位数是37.410,我把去头去尾后的均值与中位数对照主要是想说明这个均值不像全样本均值那样非常偏右,如果要选一个数值作为这组数字的代表的话,这个均值应该比全样本均值更合适一些,因为它删除了少量极端值的影响。
不过这只是一个经验方法,不知道是不是有更合理的方法呢?
楼主写了这么多,谢谢分享
明白了。“去头去尾后”的均值是46.123、中位数是37.410,这样是很厉害的异常值删除方法(可能删得也比较多),结果估计是比较“均匀”的分布。
楼主的页面停留时间其实应该叫做页面间隔,并不是实际页面停留时间。
建议看看这个介绍:
http://www.adjyc.com/file/Cnzz-Baidu-JYC-vs.pdf